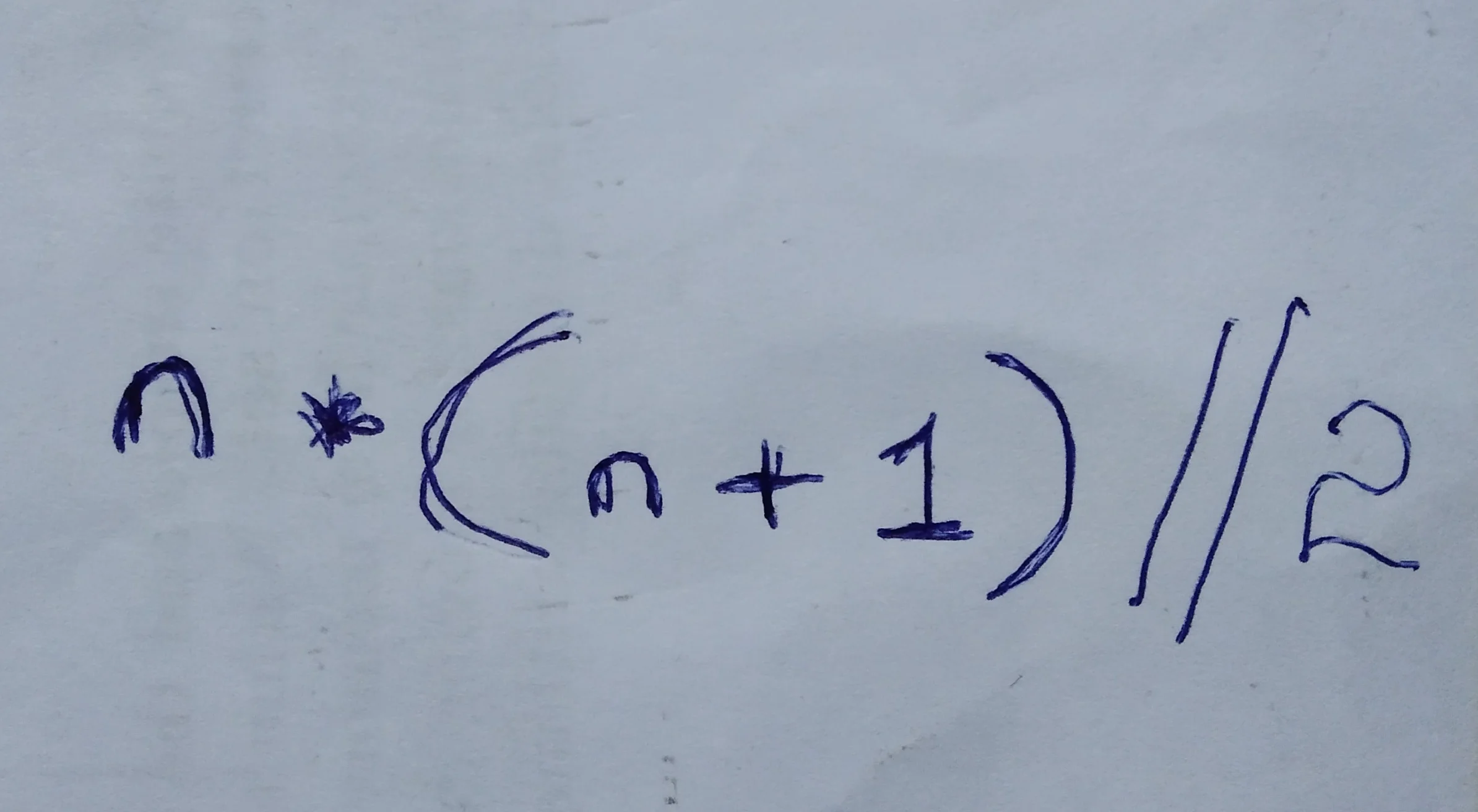Gauss’s Formula: The Arithmetic Series Formula [n*(n+1) / 2]

Carl Friedrich Gauss, one of the most renowned mathematicians of all time, in his early years, during his time in elementary school was tasked with a seemingly mundane problem – summing the numbers from 1 to 100.

Gauss’s solution to this problem not only impressed his teacher but also led to the discovery of a fundamental mathematical concept – the arithmetic series formula.

S_n = (n(n+1))/2

S_n: Sum of the first n natural numbers.

n: The number of terms in the sequence.
n+1: The next number in the sequence (the natural number immediately following n.
2: A constant factor in the formula that divides the result to calculate the sum.

This formula specifically calculates the sum of the first (n) natural numbers starting from 1. However, if you have a sequence of consecutive numbers that doesn’t start from 1, you’ll need to use the more general arithmetic series formula, which is given as:

S_n = (n/2) * (2a + (n-1)d)

Where n is the number of terms, a is the first term, and d is the common difference between terms.

Now let’s walk through Gauss’s elegant solution, and then delve into a more technical understanding of how the formula works.

Gauss Arithmetic Series Formula

The Story of Gauss

Carl Friedrich Gauss, often referred to as the “Prince of Mathematicians,” left an indelible mark on the world of mathematics.

A captivating story from his early years epitomizes his extraordinary mathematical insight.

Gauss’s Arithmetic Revelation

The challenge presented to Gauss was deceptively simple: add all the integers from 1 to 100.

His teacher likely expected this task to keep the students occupied with busywork.

However, Gauss’s solution was nothing short of brilliant.

How Gauss Solved the Problem

Gauss noticed that he could flip the sequence and group the numbers differently.

Instead of summing 1 + 2 + 3 + ... + 100, he rearranged it as 100 + 99 + 98 + ... + 1.

He paired the numbers, recognizing that each pair had the same sum. For example, 1 + 100, 2 + 99, 3 + 98, and so on, all summed to 101.
Gauss observed that there were 50 pairs of 101.
By multiplying the number of pairs (50) by the sum of each pair (101), he obtained the total sum of the sequence: 50 * 101 = 10, 100.
To find the sum from 1 to 100, he divided this result by 2, arriving at *5, 050“.

…

The formula Gauss used to solve this problem is the sum of an arithmetic series formula, which is expressed as:

sum = n*(n+1) / 2

*Here’s a breakdown of each component of the formula:“

**Sum””: This represents the total sum of the sequence.
n: The number of terms in the sequence.

Why Gauss’s Formula Works

Gauss’s insight was to realize that when you add consecutive numbers, you can pair them in such a way that each pair has the same sum.

By multiplying the number of pairs n*(n + 1) / 2 by the sum of each pair, you obtain the total sum of the sequence.

Applications in Mathematics

Gauss’s formula for the sum of an arithmetic series has far-reaching implications in mathematics.

It enables quick calculations for the sum of any arithmetic series, regardless of the number of terms.

This formula is widely used in various mathematical disciplines, from calculus to number theory and combinatorics.

In mathematical notation, the formula can be expressed as:

S_n = (n/2) * (2a + (n-1)d)

Where ‘n’ is the number of terms, ‘a’ is the first term, and ‘d’ is the common difference between terms.

Beyond Mathematics

Gauss’s formula is not confined to the realm of mathematics alone.

It finds practical applications in fields such as computer science, economics, and physics.

In computer science, it plays a critical role in algorithms for optimizing data processing.
In economics, the formula is employed to calculate the present value of cash flows, aiding in investment decisions.
In physics, it helps calculate the area under curves, making it indispensable for analyzing physical phenomena.

Conclusion

Carl Friedrich Gauss’s arithmetic series formula is a remarkable tool in mathematics that simplifies the sum of a sequence of consecutive numbers.

Gauss’s insight emphasizes the power of elegant mathematical solutions.

Understanding this formula can simplify complex calculations and prove invaluable in various mathematical disciplines and practical applications beyond math.

Gauss’s genius continues to inspire mathematicians and problem solvers, emphasizing the beauty of simplicity and efficiency in mathematics and its real-world applications.

Additions and Technical Explanation

Gauss’s formula allows us to efficiently calculate the sum of a sequence of numbers by avoiding the need to add them individually.

The formula leverages the properties of arithmetic progressions, which are sequences where each term is obtained by adding a fixed difference, known as the common difference, to the previous term.

When we add consecutive numbers, such as 1 + 2 + 3 + ... + 100, we can see that it forms an arithmetic progression with a common difference of 1.

The formula simplifies the calculation by finding the average and then multiplies it by the number of terms n.

This multiplication is essentially finding the sum of all the terms without the need to add them individually.

So, in the case of adding the numbers from 1 to 100, the formula calculates:

` Sum = 100 * (100 + 1) / 2 = 100 * 101 / 2 = 5, 050. |

This approach saves time and effort, especially when dealing with longer sequences of consecutive numbers.

Gauss’s insight into this method is a testament to his mathematical brilliance and continues to be a valuable tool in various mathematical and real-world applications.